КВАНТОВАЯ И КЛАССИЧЕСКАЯ
МЕХАНИКА
В ПРЕДСТАВЛЕНИИ ФАЗОВОГО ПРОСТРАНСТВА
Ю. M. Широков
Научно-исследовательский институт ядерной физики МГУ, Москва
Теория гамильтоновых механических систем изложена на языке только таких физических и математических понятий, которые имеют смысл как в классической, так и в квантовой механике. В частности, наблюдаемые в обеих механиках являются с-числовыми функциями координат и импульсов. Операции обычного умножения наблюдаемых и скобки Пуассона, также трактуемые как разновидности операций умножения, выделены в отдельные объекты, которые могут обладать структурными свойствами, включая зависимость от 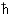 . При этом оказывается, что единственным первичным отличием квантовой механики от классической является конкретная форма одного алгебраического тождества для операций умножения. Все остальные различия получаются как вторичные.
Развитый в работе формализм особенно удобен для квантований и для переходов к классике (в том числе частичных). Переходы в обоих направлениях прозрачны и поддаются исследованию для любых величин на любом этапе выкладок. Построена единая квантово-классическая теория рассеяния. Получено интегральное квантовое уравнение типа Липпмана - Швингера, в котором роль свободного решения играет решение соответствующей классической задачи. Итерирование этого уравнения дает квантовые поправки к классическим решениям. . При этом оказывается, что единственным первичным отличием квантовой механики от классической является конкретная форма одного алгебраического тождества для операций умножения. Все остальные различия получаются как вторичные.
Развитый в работе формализм особенно удобен для квантований и для переходов к классике (в том числе частичных). Переходы в обоих направлениях прозрачны и поддаются исследованию для любых величин на любом этапе выкладок. Построена единая квантово-классическая теория рассеяния. Получено интегральное квантовое уравнение типа Липпмана - Швингера, в котором роль свободного решения играет решение соответствующей классической задачи. Итерирование этого уравнения дает квантовые поправки к классическим решениям.
The theory of the hamiltonian mechanical systems has been formulated in terms of only such physical and mathematical concepts which are meaningful in both mechanics. For instance the observables in both mechanics are represented as c-number functions of coordinates and momenta. The operations of the usual multiplication of observables as well as Poisson bracket (also treated as a sort of multiplication) are singled out as separate objects which can possess their own structure including 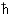 -dependence. This lead to the conclusion that the only primary distinction between classical and quantum mechanics is reduced to the distinction in the form of the algebraic identity for the multiplication operations. All other distinctions are proved to be of the secondary origin.
The formalism developed in the paper is especially useful for quantizations and for transitions (including partial ones) to the classical limits. The transitions in both directions are transparent and accessible for analysis for any quantity at any step of calculations. The unified quantum-classical scattering theory is constructed. The integral quantum Lippman - Schwinder type equation is derived where the free solution term is replaced by the solution of the corresponding classical problem. The iteration of this equation gives the quantum corrections to the classical solution. -dependence. This lead to the conclusion that the only primary distinction between classical and quantum mechanics is reduced to the distinction in the form of the algebraic identity for the multiplication operations. All other distinctions are proved to be of the secondary origin.
The formalism developed in the paper is especially useful for quantizations and for transitions (including partial ones) to the classical limits. The transitions in both directions are transparent and accessible for analysis for any quantity at any step of calculations. The unified quantum-classical scattering theory is constructed. The integral quantum Lippman - Schwinder type equation is derived where the free solution term is replaced by the solution of the corresponding classical problem. The iteration of this equation gives the quantum corrections to the classical solution.
Full text in PDF (4.148.576)
|
 Home
Home
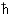 . При этом оказывается, что единственным первичным отличием квантовой механики от классической является конкретная форма одного алгебраического тождества для операций умножения. Все остальные различия получаются как вторичные.
Развитый в работе формализм особенно удобен для квантований и для переходов к классике (в том числе частичных). Переходы в обоих направлениях прозрачны и поддаются исследованию для любых величин на любом этапе выкладок. Построена единая квантово-классическая теория рассеяния. Получено интегральное квантовое уравнение типа Липпмана - Швингера, в котором роль свободного решения играет решение соответствующей классической задачи. Итерирование этого уравнения дает квантовые поправки к классическим решениям.
. При этом оказывается, что единственным первичным отличием квантовой механики от классической является конкретная форма одного алгебраического тождества для операций умножения. Все остальные различия получаются как вторичные.
Развитый в работе формализм особенно удобен для квантований и для переходов к классике (в том числе частичных). Переходы в обоих направлениях прозрачны и поддаются исследованию для любых величин на любом этапе выкладок. Построена единая квантово-классическая теория рассеяния. Получено интегральное квантовое уравнение типа Липпмана - Швингера, в котором роль свободного решения играет решение соответствующей классической задачи. Итерирование этого уравнения дает квантовые поправки к классическим решениям.