О НОВЫХ И СТАРЫХ СИММЕТРИЯХ УРАВНЕНИЙ МАКСВЕЛЛА И ДИРАКА
В. И. Фущич, А. Г. Никитин
Институт математики АН УССР, Киев
Анализируются симметрийные свойства уравнений Максвелла для электромагнитного поля, а также уравнений Дирака и Кеммера - Дэффина - Петье. В рамках "нелиевского" подхода показано, что помимо хорошо известной инвариантности относительно конформной группы и преобразований Хевисайда-Лармора-Райнича уравнения Максвелла обладают дополнительнойсимметрией относительно группы U(2) 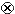 U(2) и относительно 23-мерной алгебры Ли А23. Преобразования дополнительной симметрии задаются нелокальными интегро-дифференциальными операторами. Исследована симметрия уравнения Дирака в классе дифференциальных и интегро-дифференциальных преобразований. Показано, что это уравнение инвариантно относительно 18-параметрической группы, включающей в качестве подгруппы группу Пуанкаре. Найдена 28-параметрическая группа инвариантности уравнения Кеммера-Дэффина-Петье.
Получены конечные преобразования из конформной группы для безмассового поля с произвольным спином. Приведен явный вид конформных преобразований для электромагнитного поля, а также для полей Дирака и Вейля. U(2) и относительно 23-мерной алгебры Ли А23. Преобразования дополнительной симметрии задаются нелокальными интегро-дифференциальными операторами. Исследована симметрия уравнения Дирака в классе дифференциальных и интегро-дифференциальных преобразований. Показано, что это уравнение инвариантно относительно 18-параметрической группы, включающей в качестве подгруппы группу Пуанкаре. Найдена 28-параметрическая группа инвариантности уравнения Кеммера-Дэффина-Петье.
Получены конечные преобразования из конформной группы для безмассового поля с произвольным спином. Приведен явный вид конформных преобразований для электромагнитного поля, а также для полей Дирака и Вейля.
Symmetry properties of the Maxwell equation for the electromagnetic field are analysed as well as of the Dirac and Kemmer - Duffin - Petiau one.
In the frame of the non-geometrical approach it is demonstrated, that besides to the well-known invariance under the conformal group and Heaviside - Larmor - Rainich transformation, Maxwell equations possess the additional symmetry under the group U(2) 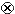 U(2) and under the 23-dimensional Lie algebra A23. The additional symmetry transformations are realized by the non-local (integro-differential) operators.
The symmetry of the Dirac equation under the differential and integro-differential transformations is investigated. It is shown, that this equation is invariant under the 18-parametrical group, which includes the Poincare group as a subgroup.
The 28-parametrical invariance group of the Kemmer - Duffin - Petiau equation is found.
The finite conformal group transformations for a massless field of any spin are obtained. The explicit form of the conformal transformations for the electromagnetic field as well as for the Dirac and Weyl fields is given. U(2) and under the 23-dimensional Lie algebra A23. The additional symmetry transformations are realized by the non-local (integro-differential) operators.
The symmetry of the Dirac equation under the differential and integro-differential transformations is investigated. It is shown, that this equation is invariant under the 18-parametrical group, which includes the Poincare group as a subgroup.
The 28-parametrical invariance group of the Kemmer - Duffin - Petiau equation is found.
The finite conformal group transformations for a massless field of any spin are obtained. The explicit form of the conformal transformations for the electromagnetic field as well as for the Dirac and Weyl fields is given.
Full text in PDF (2.204.071)
|
 Home
Home
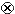 U(2) и относительно 23-мерной алгебры Ли А23. Преобразования дополнительной симметрии задаются нелокальными интегро-дифференциальными операторами. Исследована симметрия уравнения Дирака в классе дифференциальных и интегро-дифференциальных преобразований. Показано, что это уравнение инвариантно относительно 18-параметрической группы, включающей в качестве подгруппы группу Пуанкаре. Найдена 28-параметрическая группа инвариантности уравнения Кеммера-Дэффина-Петье.
Получены конечные преобразования из конформной группы для безмассового поля с произвольным спином. Приведен явный вид конформных преобразований для электромагнитного поля, а также для полей Дирака и Вейля.
U(2) и относительно 23-мерной алгебры Ли А23. Преобразования дополнительной симметрии задаются нелокальными интегро-дифференциальными операторами. Исследована симметрия уравнения Дирака в классе дифференциальных и интегро-дифференциальных преобразований. Показано, что это уравнение инвариантно относительно 18-параметрической группы, включающей в качестве подгруппы группу Пуанкаре. Найдена 28-параметрическая группа инвариантности уравнения Кеммера-Дэффина-Петье.
Получены конечные преобразования из конформной группы для безмассового поля с произвольным спином. Приведен явный вид конформных преобразований для электромагнитного поля, а также для полей Дирака и Вейля.