НЕСТАНДАРТНЫЕ АЛГЕБРЫ ОПЕРАТОРОВ РОЖДЕНИЯ-УНИЧТОЖЕНИЯ И ПРОМЕЖУТОЧНЫЕ КВАНТОВЫЕ СТАТИСТИКИ
С. А. Балашова, В. В. Курышкин
Университет дружбы народов, Москва
Э. Э. Энтральго
Объединенный институт ядерных исследований, Дубна
Обсуждаются проблемы математического описания систем переменного числа физических объектов сортов k, подчиняющихся квантовым статистикам рангов sk в том смысле, что числа nk объектов сорта k в одном квантовом состоянии могут принимать значения лишь от 0 до k.
Предложен метод построения алгебры А(К) взаимно сопряженным образующим a+k и ak, k 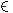 К, которой может быть приписан физический смысл операторов рождения и уничтожения объекта сорта k. К, которой может быть приписан физический смысл операторов рождения и уничтожения объекта сорта k.
Построен ряд конкретных алгебр операторов рождения - уничтожения, проведено сравнение с уже известными алгебрами, рассмотрены некоторые приложения промежуточных (2  sk < sk < 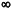 ) квантовых статистик. ) квантовых статистик.
The problems of mathematical description for systems of a variable number of physical objects of types k which obey to quantum statistics of ranks sk, that is numbers nk for objects of type k can take in the same quantum state the values only from 0 to sk are discussed.
A method to construct the algebras A(K) with selfadjoint generators a+k and ak k 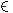 К which can be treated as the creation and annihilation operators for the object of type k is proposed. К which can be treated as the creation and annihilation operators for the object of type k is proposed.
A set of concrete algebras of the creation and annihilation operators is constructed, a comparison with the already known algebras is performed, some applications of the intermediate (2  sk < sk < 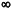 ) quantum statistics are considered. ) quantum statistics are considered.
Full text in PDF (2.140.950)
|
 Home
Home
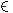 К, которой может быть приписан физический смысл операторов рождения и уничтожения объекта сорта k.
К, которой может быть приписан физический смысл операторов рождения и уничтожения объекта сорта k.  sk <
sk < 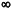 ) квантовых статистик.
) квантовых статистик.