УДК 530.12:531.51
Введение геометрии Лобачевского в теорию гравитации. Черников Н.A. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1155.
Весь ученый мир празднует в 1992 г. двухсотлетнюю годовщину со дня рождения Николая Ивановича Лобачевского. Этому событию посвящается данный обзор. В нем приведены краткие сведения о великом ученом и об открытии им неевклидовой геометрии. Рассмотрено отношение Императорской Санкт-Петербургской Академии наук и Геттингенского Королевского общества наук к самому Лобачевскому и к его геометрии. Цитированы отрывки из писем Гаусса, в которых говорится о неевклидовой геометрии. Дано краткое изложение основ геометрии Лобачевского. Рассмотрено, какого рода перемена происходит от введения геометрии Лобачевского в небесную механику. Подробно рассмотрена перемена, введенная Лобачевским в закон всемирного тяготения Ньютона. Решена задача Кеплера о движении планеты в пространстве Лобачевского. Дано определение планетной орбиты, не зависящее от постулата Евклида о параллельных прямых линиях в видимом нами мире.
В обзоре содержится извлечение из мастерски написанного В.Я.Буняковским сочинения "Параллельные линии" (СПб, 1853), по которому можно судить о состоянии, в котором находилась бы геометрия, если открытие Лобачевского осталось бы недоступным уму человеческому. Но уже Ф.М.Достоевский заметил, что в меру понимания неевклидовой геометрии сам ум человеческий становился неевклидовским. В этом таится ответ на загадку, почему над решением проблемы параллельных, казалось бы, почти безуспешно, трудилось так много поколений ученых всех стран мира.
Библиогр.: 54 назв.

УДК 539.12.01
Проявление структуры вакуума КХД в составных кварковых моделях. Дорохов А.Е., Зубов Ю,А., Кочелев Н.И. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1192.
Существуют три основных подхода " проблеме расщепления масс внутри адронных мультиплетов. Во-первых, нерелятивистская кварковая модель, в которой расщепление определяется разностью масс конституентных кварков и зависимостью потенциала Брейта - Ферми от масс кварков. Во-вторых, различные версии модели мешков объясняют этот эффект с помощью разности токовых масс кварков и зависимостью потенциала одноглюонного обмена от аромата кварков. Однако связь этих подходов с теорией сильных взаимодействий КХД выглядит проблематичной. Это стало особенно ясно после появления метода правил сумм (ПС) КХД, который основан на первых принципах теории. В этом подходе основной вклад в расщепление масс дает учет взаимодействия с КХД-вакуумом.
В этом обзоре рассматривается версия модели мешков, в которой учитывается взаимодействие кварков с вакуумом КХД внутри адрона. Как известно, вакуум КХД имеет сложную стуктуру. В модели инетантонной жидкости коротковолновые вакуумные флуктуации определяются инстантонами с эффективным радиусом r_с = 1,5 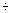2 ГэВ, а длинноволновые флуктуации обусловлены коллективными возбуждениями инетантонной жидкости, которые характеризуются значением глюонного конденсата. Таким образом, рассматривается модель адронов, в которой кварковый мешок погружен в инстантонный вакуум.
Взаимодействие кварков с конденсатными полями, которое генерируется сдвигом в лагранжиане модели полей в мешке на вакуумные (классические) компоненты полей, дает вклад в энергию адрона вида DE_vас = - S_flavors N_i A(c_i, m_i) (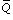_i Q_i)R². Этот вклад стабилизирует мешок от развала, определяет масштаб адронных масс и решает проблему сохранения энергии в модели.
Взаимодействие кварков с инстантонами малого размера аппроксимируется эффективным четырехкварковым лагранжианом т' Хоофта, который имеет следующую спин-аромат-цветовую структуру: DL_inst [1 + 3/32 l^с l^с(1 - 3/4 s^s s^s)] (1 - t^f t^f ). Кварки взаимодействуют через обмен инстантонами как внутри мешка, так и на его поверхности. Последнее гарантирует сохранение изотриплетного аксиального тока и в то же время учитывает аксиальную аномалию в синглетном канале.
В рамках этой модели объяснены основные особенности спектра адронов, такие как (N - D)-, (p - r)- и изоспиновые расщепления, решение U_A(1) проблемы. Получен общий вид взаимодействия через инстантоны для произвольных мультикварковых состояний. Изучено влияние взаимодействия с вакуумными полями на статические свойства адронов. Учтен вклад моря кварков в протоне и дана оценка этого вклада в спин протона.
Табл. 9. Илл. 11. Библиогр.: 105 назв.

УДК 537.8
Электромагнитные свойства тороидальных соленоидов. Афанасьев Г.Н. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1264.
В обзоре рассмотрены основные свойства тороидальных и цилиндрических соленоидов. Затронуты следующие вопросы: электромагнитные поля соленоидов с постоянным и переменным токами, с различными магнетизациями; мультипольное разложение электромагнитного поля тороидальных соленоидов, связь тороидальных моментов с традиционными; взаимодействие соленоидов с внешним электромагнитным полем и друг с другом. На примере цилиндрического соленоида показано, что при равномерном движении соленоида в среде электромагнитное поле выходит за его пределы. Получено электромагнитное поле вращающегося тороидального соленоида. Указаны возможные применения соленоидов в физике и технике.
Ил. 10. Библиогр.: 43 назв.

УДК 539.12.01
Расходимости в двумерных нелинейных сигма-моделях. Белокуров В.В., Казаков Д.И. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1322.
Исследования структуры ультрафиолетовых расходимостей двумерных нелинейных сигма-моделей, инициированные потребностями теории струн, приобретают в настоящее время более широкое значение. В связи с этим возрастает роль методов вычисления в двумерных нелинейных теориях.
Настоящий обзор содержит детальное описание методов вычисления ультрафиолетовых расходимостей в этих теориях. Приводятся сведения о геометрии полевых многообразий и вводится понятие обобщенной перенормируемости сигма-модели. Излагается ковари-антный метод фонового поля в нелинейной теории. Обсуждаются проблема инфракрасных расходимостей и способы их устранения. Иллюстрацией служат двух петле вые расчеты в бо-зонной сигма-модели с членом Весса - Зумино, а также четырех- и пятипетлевые расчеты в суперсимметричной N = 1 и N = 2 сигма-модели. В заключение обсуждается роль риччи-плоских многообразий для построения конформно-инвариантных двумерных теорий.
Данный обзор может служить своего рода пособием по методам вычислений расходи-мостей в двумерных теориях. Для этого изложение сделано максимально подробным и значительное место в нем уделено конкретным расчетам, которые, как правило, сопровождаются детальными промежуточными выкладками.
Табл. 2. Ил. 9. Библиогр.: 72 назв.

УДК 530.19+ 535.361
Дискретная и непрерывная квантовая механика, точно решаемые модели (Уроки квантовой интуиции II). Захарьев Б.Н. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1387.
Обзор подытоживает серию исследований по "квантовой инженерии" и является продолжением предыдущего (ЭЧАЯ, 1990, т. 21, с.914). Приводятся "квантовые картинки", проясняющие специфику движения волн по решеткам (каналов, конфигураций), что позволяет с качественно новой стороны взглянуть на структуру связанных состояний и механизмы рассеяния: какое нужно выбрать взаимодействие, чтобы создать желаемый спектр или резонансную картину. Подход обратной задачи пополняет арсенал квантовой теории. Демонстрируются неожиданные проявления невидимой верхней (по энергии) границы разрешенной зоны в дискретном представлении волновой функции (например, запирание волн на потенциальном склоне), роль "уравнений Шредингера высшего ( 4) порядка", новые точно решаемые модели, разрыв непрерывного спектра запрещенной зоной (лакуной) в заранее заданном месте с помощью периодического возмущающего потенциала специального вида. Все это как бы перекидывает мостик между ядерной (атомной) и твердотельной квантовой физикой.
Ил. 63. Библиогр.: 91 назв.

УДК 681.518.3
Электронные методы в экспериментальной физике высоких энергий. Никитюк Н.М. Физика элементарных частиц и атомного ядра. 1992, том 23, вып. 6, с. 1469.
В обзоре рассматриваются современное состояние и перспективы развития электронных методов в физике высоких и сверхвысоких энергий. Основное внимание уделяется описанию широкого спектра детекторов заряженных частиц, применяемых как в экспериментах с фиксированной мишенью, так и на коллайдерах. Описаны методы детектирования, регистрации и передачи световых сигналов с помощью волоконных и сцинтилляционых волоконных световодов, шифтеров, ФЭУ различных конструкций и микроканальных пластин. Приведен ряд схем, применяемых для считывания световых сигналов от модулей калориметров. Рассмотрены вопросы применения в экспериментах таких перспективных приборов, как кремниевые детекторы и мониторы, создаваемые на базе микрополосковых кремниевых детекторов, ПЗС-матриц и пиксель-детекторов. Подробно описаны параметры и методы съема информации, регистрируемой в трех координатных газовых детекторах. В частности, рассмотрено применение таких детекторов, как времяпроекционные камеры, "образные" дрейфовые камеры, мультидрейфовые и векторные трехкоординатные газонаполненные детекторы. В заключение приводится описание специализированных микросхем, применяемых в ядерной электронике, обсуждаются методы обработки трековой информации в реальном времени, в том числе с использованием нейроноподобных сетей, и калориметрические триггеры.
Табл. 1. Ил. 22. Библиогр.: 205 назв.