ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ ВОЗБУЖДЕНИЯ ЯДЕРНОЙ ПЛОТНОСТИ
В. Г. Картавенко
Объединенный институт ядерных исследований, Дубна
Обзор посвящен развитию методов описания нелинейных явлений и процессов релаксации в сложных ядерных системах, образующихся при взаимодействии тяжелых ионов с атомными ядрами при энергиях 10 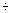 100 МэВ/нуклон. Для анализа линейных и нелинейных возбуждений ядерной плотности развит вариант ядерной гидродинамики, основанный на алгебре токов и плотностей. Показано, что для безвихревого движения в квазиклассическом пределе уравнения ядерной гидродинамики можно свести к нелинейному уравнению Шредингера. Показано, что сферически-симметричные односолитонные решения хорошо описывают свойства ядерной плотности в основном состоянии. Указано на возможность существования сферически-симметричных узловых состояний ядерной плотности. Получены аналитические решения для одномерных нелинейных возбуждений: "кноидальные" волны, "кинки", "дырки" в ядерной материи. Получены основные уравнения для описания вихревых "дисков" ядерного вещества. Эволюция границы "диска" аналогична распространению в плоскости нелинейной дисперсной волны. Проведен качественный анализ основных свойств "дисковых" состояний. Метод обратной задачи для среднего поля ядра использован для анализа статических (описание профилей плотности и одночастичных потенциалов) и динамических (простая модель для анализа эволюции сжатого в начальный момент ядра) свойств ядерных систем. Показано, что монопольные изоскалярные гигантские резонансы можно рассматривать как линеаризованные колебания солитона ядерной плотности. Построено аналитическое самосогласованное решение для колебаний двойной ядерной системы. Исследовано влияние канала когерентного возбуждения гигантских резонансов на процесс эмиссии неравновесных легких частиц и явление диссипации кинетической энергии. 100 МэВ/нуклон. Для анализа линейных и нелинейных возбуждений ядерной плотности развит вариант ядерной гидродинамики, основанный на алгебре токов и плотностей. Показано, что для безвихревого движения в квазиклассическом пределе уравнения ядерной гидродинамики можно свести к нелинейному уравнению Шредингера. Показано, что сферически-симметричные односолитонные решения хорошо описывают свойства ядерной плотности в основном состоянии. Указано на возможность существования сферически-симметричных узловых состояний ядерной плотности. Получены аналитические решения для одномерных нелинейных возбуждений: "кноидальные" волны, "кинки", "дырки" в ядерной материи. Получены основные уравнения для описания вихревых "дисков" ядерного вещества. Эволюция границы "диска" аналогична распространению в плоскости нелинейной дисперсной волны. Проведен качественный анализ основных свойств "дисковых" состояний. Метод обратной задачи для среднего поля ядра использован для анализа статических (описание профилей плотности и одночастичных потенциалов) и динамических (простая модель для анализа эволюции сжатого в начальный момент ядра) свойств ядерных систем. Показано, что монопольные изоскалярные гигантские резонансы можно рассматривать как линеаризованные колебания солитона ядерной плотности. Построено аналитическое самосогласованное решение для колебаний двойной ядерной системы. Исследовано влияние канала когерентного возбуждения гигантских резонансов на процесс эмиссии неравновесных легких частиц и явление диссипации кинетической энергии.
A review of the nonlinear phenomena and relaxation processes in the low and intermediate energy (E ~ 10 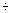 100 MeV/nucleon) nucleus-nucleus collisions is given. Current and density algebra approach to nuclear hydrodynamics is proposed to describe linear and nonlinear excitations of the nuclear density. In a semiclassical limit the main equations have been reduced to the nonlinear Schr 100 MeV/nucleon) nucleus-nucleus collisions is given. Current and density algebra approach to nuclear hydrodynamics is proposed to describe linear and nonlinear excitations of the nuclear density. In a semiclassical limit the main equations have been reduced to the nonlinear Schr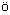 dinger equation for irrotational flow motion. The nodeless spherical symmetrical soliton-type solutions describe well the main properties of a nuclear density in a ground state. It is pointed out that there may exist a nodal isomer state (a first nonlinear excitation) of the nuclear density. The following analytical one-dimensional solutions: soliton-like solutions (describing nuclear "slabs"), periodical nonlinear oscillations (analogue to "cnoidal"-type waves in plasma), a small amplitude nonlinear wave (subsonic "hole"-like localized pulse), exact solutions under nonvanishing boundary conditions ("kinks", "holes") have been derived. The basic equations for the nonlinear nuclear vortical "disks" have been constructed. The evolution of the shape of the vortex is analogous to the propagation of a nonlinear dispersion wave in plane. A qualitative analysis of the main features of the vortex is done. Inverse mean field method has been used to analyze the statical (density profiles and single particle potentials) and dynamical (a simple model to descride an evolution of the initially compressed nuclei) properties of the nuclear systems. It is shown the monopole isoscalar density giant resonances can be considered as the linearized soliton oscillations. An analytical solution to describe the self-consistent two-center nuclear density oscillations is constructed. An influence of the coherent giant resonances channel on the light particle emission processes and dissipation phenomena is investigated. dinger equation for irrotational flow motion. The nodeless spherical symmetrical soliton-type solutions describe well the main properties of a nuclear density in a ground state. It is pointed out that there may exist a nodal isomer state (a first nonlinear excitation) of the nuclear density. The following analytical one-dimensional solutions: soliton-like solutions (describing nuclear "slabs"), periodical nonlinear oscillations (analogue to "cnoidal"-type waves in plasma), a small amplitude nonlinear wave (subsonic "hole"-like localized pulse), exact solutions under nonvanishing boundary conditions ("kinks", "holes") have been derived. The basic equations for the nonlinear nuclear vortical "disks" have been constructed. The evolution of the shape of the vortex is analogous to the propagation of a nonlinear dispersion wave in plane. A qualitative analysis of the main features of the vortex is done. Inverse mean field method has been used to analyze the statical (density profiles and single particle potentials) and dynamical (a simple model to descride an evolution of the initially compressed nuclei) properties of the nuclear systems. It is shown the monopole isoscalar density giant resonances can be considered as the linearized soliton oscillations. An analytical solution to describe the self-consistent two-center nuclear density oscillations is constructed. An influence of the coherent giant resonances channel on the light particle emission processes and dissipation phenomena is investigated.
Full text in PDF (2.044.585)
|
 Home
Home
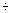 100 МэВ/нуклон. Для анализа линейных и нелинейных возбуждений ядерной плотности развит вариант ядерной гидродинамики, основанный на алгебре токов и плотностей. Показано, что для безвихревого движения в квазиклассическом пределе уравнения ядерной гидродинамики можно свести к нелинейному уравнению Шредингера. Показано, что сферически-симметричные односолитонные решения хорошо описывают свойства ядерной плотности в основном состоянии. Указано на возможность существования сферически-симметричных узловых состояний ядерной плотности. Получены аналитические решения для одномерных нелинейных возбуждений: "кноидальные" волны, "кинки", "дырки" в ядерной материи. Получены основные уравнения для описания вихревых "дисков" ядерного вещества. Эволюция границы "диска" аналогична распространению в плоскости нелинейной дисперсной волны. Проведен качественный анализ основных свойств "дисковых" состояний. Метод обратной задачи для среднего поля ядра использован для анализа статических (описание профилей плотности и одночастичных потенциалов) и динамических (простая модель для анализа эволюции сжатого в начальный момент ядра) свойств ядерных систем. Показано, что монопольные изоскалярные гигантские резонансы можно рассматривать как линеаризованные колебания солитона ядерной плотности. Построено аналитическое самосогласованное решение для колебаний двойной ядерной системы. Исследовано влияние канала когерентного возбуждения гигантских резонансов на процесс эмиссии неравновесных легких частиц и явление диссипации кинетической энергии.
100 МэВ/нуклон. Для анализа линейных и нелинейных возбуждений ядерной плотности развит вариант ядерной гидродинамики, основанный на алгебре токов и плотностей. Показано, что для безвихревого движения в квазиклассическом пределе уравнения ядерной гидродинамики можно свести к нелинейному уравнению Шредингера. Показано, что сферически-симметричные односолитонные решения хорошо описывают свойства ядерной плотности в основном состоянии. Указано на возможность существования сферически-симметричных узловых состояний ядерной плотности. Получены аналитические решения для одномерных нелинейных возбуждений: "кноидальные" волны, "кинки", "дырки" в ядерной материи. Получены основные уравнения для описания вихревых "дисков" ядерного вещества. Эволюция границы "диска" аналогична распространению в плоскости нелинейной дисперсной волны. Проведен качественный анализ основных свойств "дисковых" состояний. Метод обратной задачи для среднего поля ядра использован для анализа статических (описание профилей плотности и одночастичных потенциалов) и динамических (простая модель для анализа эволюции сжатого в начальный момент ядра) свойств ядерных систем. Показано, что монопольные изоскалярные гигантские резонансы можно рассматривать как линеаризованные колебания солитона ядерной плотности. Построено аналитическое самосогласованное решение для колебаний двойной ядерной системы. Исследовано влияние канала когерентного возбуждения гигантских резонансов на процесс эмиссии неравновесных легких частиц и явление диссипации кинетической энергии.
 dinger equation for irrotational flow motion. The nodeless spherical symmetrical soliton-type solutions describe well the main properties of a nuclear density in a ground state. It is pointed out that there may exist a nodal isomer state (a first nonlinear excitation) of the nuclear density. The following analytical one-dimensional solutions: soliton-like solutions (describing nuclear "slabs"), periodical nonlinear oscillations (analogue to "cnoidal"-type waves in plasma), a small amplitude nonlinear wave (subsonic "hole"-like localized pulse), exact solutions under nonvanishing boundary conditions ("kinks", "holes") have been derived. The basic equations for the nonlinear nuclear vortical "disks" have been constructed. The evolution of the shape of the vortex is analogous to the propagation of a nonlinear dispersion wave in plane. A qualitative analysis of the main features of the vortex is done. Inverse mean field method has been used to analyze the statical (density profiles and single particle potentials) and dynamical (a simple model to descride an evolution of the initially compressed nuclei) properties of the nuclear systems. It is shown the monopole isoscalar density giant resonances can be considered as the linearized soliton oscillations. An analytical solution to describe the self-consistent two-center nuclear density oscillations is constructed. An influence of the coherent giant resonances channel on the light particle emission processes and dissipation phenomena is investigated.
dinger equation for irrotational flow motion. The nodeless spherical symmetrical soliton-type solutions describe well the main properties of a nuclear density in a ground state. It is pointed out that there may exist a nodal isomer state (a first nonlinear excitation) of the nuclear density. The following analytical one-dimensional solutions: soliton-like solutions (describing nuclear "slabs"), periodical nonlinear oscillations (analogue to "cnoidal"-type waves in plasma), a small amplitude nonlinear wave (subsonic "hole"-like localized pulse), exact solutions under nonvanishing boundary conditions ("kinks", "holes") have been derived. The basic equations for the nonlinear nuclear vortical "disks" have been constructed. The evolution of the shape of the vortex is analogous to the propagation of a nonlinear dispersion wave in plane. A qualitative analysis of the main features of the vortex is done. Inverse mean field method has been used to analyze the statical (density profiles and single particle potentials) and dynamical (a simple model to descride an evolution of the initially compressed nuclei) properties of the nuclear systems. It is shown the monopole isoscalar density giant resonances can be considered as the linearized soliton oscillations. An analytical solution to describe the self-consistent two-center nuclear density oscillations is constructed. An influence of the coherent giant resonances channel on the light particle emission processes and dissipation phenomena is investigated.