|
C. Grosche II. Institut f 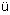 r Theoretische Physik, Universitat Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany r Theoretische Physik, Universitat Hamburg, Luruper Chaussee 149, 22761 Hamburg, Germany
G. S. Pogosyan, A. N.Sissakian Joint Institute for Nuclear Research, 141980 Dubna, Moscow Region, Russia
In the present paper on superintegrable potentials on spaces of constant curvature we discuss the case of the three-dimensional hyperboloid. Whereas in many coordinate systems an explicit path integral solution for the corresponding potential is impossible, we list in the soluble cases the path integral solutions explicitly in terms of the propagators and the spectral expansions into the wave-functions. We find the analogues of the maximally and minimally superintegrable potentials of
В настоящей статье, посвященной задачам с суперинтегрируемыми потенциалами в пространствах постоянной кривизны, обсуждается случай трехмерного гиперболоида. Несмотря на невозможность точного решения соответствующих задач с помощью метода континуального интегрирования во многих разделяющих системах координат в работе приведены все случаи, когда это удается сделать точно для пропагаторов и спектральных разложений по волновым функциям. Построены аналоги максимально и минимально суперинтегрируемых потенциалов в |
 Home
Home
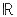 3 on the hyperboloid and many minimally superintegrable potentials which emerge from the subgroup chains corresponding to SO(3,1). Some special care is taken for the proper generalization of the harmonic oscillator and the Kepler problem.
3 on the hyperboloid and many minimally superintegrable potentials which emerge from the subgroup chains corresponding to SO(3,1). Some special care is taken for the proper generalization of the harmonic oscillator and the Kepler problem.