|
A.N.Sissakian, O.Yu.Shevchenko, S.B.Solganik Joint Institute for Nuclear Research, Dubna Developing Fock's ideas, we consider here the topological
effects in the gauge field theory.
Two closely related topological phenomena are studied
at finite density and temperature.
These are chiral anomaly and the Chern-Simons term.
It occurs that the chiral anomaly doesn't depend on
density and temperature.
The Chern-Simons term appearance in even dimensions is studied
under two types of constraints: chiral and usual charges conservation.
In odd dimensions, by using different methods,
it is shown that Развивая идеи Фока, мы рассматриваем здесь топологические эффекты в теории
калибровочных полей. Изучаются два тесно связанных топологических эффекта при
конечных плотности и температуре. Это киральная аномалия и черн-саймоновский
член. Оказывается, что киральная аномалия не зависит от температуры и
плотности. Генерация черн-саймоновского члена изучается в четномерных
пространствах при двух типах связей, отражающих сохранение кирального и
обычного зарядов. В нечетномерных пространствах при использовании различных методов
показывается, что Full text in PDF (362.482) |
 Home
Home
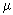 2 = m2 is the
crucial point for Chern-Simons at zero temperature.
So when
2 = m2 is the
crucial point for Chern-Simons at zero temperature.
So when