RADIALLY EXCITED SCALAR, PSEUDOSCALAR, AND VECTOR MESON NONETS IN A CHIRAL QUARK MODEL
M. K. Volkov, V. L. Yudichev
Joint Institute for Nuclear Research, Dubna, Russia
A chiral Lagrangian containing, besides the usual meson
fields, their first radial excitations is constructed. The
Lagrangian is derived by bosonization of a Nambu-Jona-Lasinio (NJL) type quark
model with separable nonlocal interactions.
The nonlocality is described by form factors
corresponding to 3-dimensional excited state wave
functions. The spontaneous breaking of chiral symmetry
is governed by the standard NJL gap equations.
A simple SU(2) x SU(2) version of the model is used to
demonstrate all low-energy theorems to hold valid in the
chiral limit.
A more realistic U(3) x U(3) model
with 't Hooft interaction is
constructed to describe the mass spectrum of excited scalar,
pseudoscalar, and vector mesons. On the basis of
global chiral symmetry, we use the same form factors for
the scalar and pseudoscalar mesons. Having fixed the form factor
parameters by masses of pseudoscalar
mesons, we predict the mass spectrum of scalar mesons. This
allows us to interpret experimentally observed scalar, pseudoscalar, and
vector meson states
as members of quark-antiquark nonets. It is shown that
the a0(1450), K0*(1430), f0(1370), fJ(1710)
scalar meson states are the first radial excitations of
the ground states: a0(980), K0*(960), f0(400-1200),
f0(980).
The weak decay constants F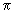 ,
F ,
F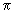 ', FK, FK' and the main strong decay widths of
the scalar, pseudoscalar, and vector meson nonets are calculated. ', FK, FK' and the main strong decay widths of
the scalar, pseudoscalar, and vector meson nonets are calculated.
Построен киральной лагранжиан, содержащий кроме обычных мезонных полей их
первые радиальные возбуждения. Лагранжиан получен бозонизацией кварковой модели типа Намбу-Иона-Лазинио (НИЛ)
с сепарабельным нелокальным взаимодействием.
Нелокальность описывается формфакторами, соответствующими трехмерным волновым
функциям возбужденных мезонов. Спонтанное нарушение киральной симметрии
определяется уравнением на щель. На простом примере SU(2) x SU(2)-версии этой модели
продемонстрировано выполнение всех низкоэнергетических теорем в
киральном пределе.
Для описания спектра масс возбужденных скалярных, псевдоскалярных и векторных
мезонов построена более реалистичная U(3) x U(3)-модель с
взаимодействием 'т Хофта. В силу глобальной киральной симметрии, мы используем
одинаковые формфакторы для скалярных и псевдоскалярных мезонов. Фиксируя
параметры формфакторов по массам псевдоскалярных мезонов, мы предсказываем
спектр масс скалярных мезонов. Это позволяет нам интерпретировать
экспериментально наблюдаемые скалярные, псевдоскалярные мезонные состояния как члены кварк-антикварковых нонетов.
Показано, что скалярные мезонные состояния
a0(1450), K0*(1430), f0(1370), fJ(1710)
являются первыми радиальными возбуждениями основных состояний
a0(980), K0*(960), f0(400-1200),
f0(980).
Вычислены константы слабых распадов
F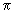 ,
F ,
F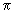 ', FK, FK'
и ширины основных сильных распадов скалярных, псевдоскалярных и векторных
нонетов мезонов. ', FK, FK'
и ширины основных сильных распадов скалярных, псевдоскалярных и векторных
нонетов мезонов.
Full text in PDF (500.714)
|
 Home
Home
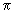 ,
F
,
F