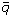BOUND q SYSTEMS IN THE FRAMEWORK OF DIFFERENT VERSIONS OF 3D REDUCTIONS OF THE BETHE-SALPETER EQUATION

T. Kopaleishvili

HEPI, Tbilisi State University, University St. 9, 380086 Tbilisi, Georgia

Five different versions of the three-dimensional (3D) reduction of the Bethe-Salpeter (BS) equation in the instantaneous approximation for kernel of BS equation for the two-fermion systems are formulated. The normalization conditions for the bound-state wave function in all versions are derived. Further, the 3D reduction of BS equation without instantaneous approximation for the kernel of BS equation is formulated in the quasi-potential approach. Except for the Salpeter version, other four versions have the correct one-body limit (Dirac equation) when mass of one of constituent fermions tends to infinity. Application of these versions for investigation of the different properties of the q bound systems are considered.

Сформулированы пять различных версий трехмерной редукции уравнения Бете-Солпитера (БС) для двухфермионной системы в одновременном приближении для ядра уравнения БС. Получены условия нормировки волновой функции связанного состояния для всех версий редукции. Сформулирована также трехмерная редукция уравнения БС в квазипотенциальном подходе без применения одновременного приближения для ядра уравнения БС. Все версии редукции имеют правильный одночастичный предел (уравнение Дирака), в котором масса одного из составляющих фермионов устремляется в бесконечность, за исключением версии Солпитера. Рассмотрено также применение этих версий для исследования различных свойств связанной q-системы.