|
С.Манов Объединенный институт ядерных исследований, Дубна В обзоре детально рассмотрена возможность введения на дифференцируемом многообразии пары контравариантной и ковариантной аффинных связностей, различающихся не только знаком. Теория пространств с такими парами связностей детально разработана здесь в объеме, необходимом для построения кинематики векторных полей и лагранжевой теории тензорных полей в таких пространствах. Введены оператор ковариантного дифференцирования и дифференциальный оператор Ли. Исследуется их действие на тензорные поля. В пространствах с разными связностями рассмотрено действие девиационного оператора, играющего существенную роль для уравнений девиации в гравитационной физике. Введены понятия ковариантной и контравариантной метрик с соответствующими им проективными метриками. Определено действие ковариантного оператора дифференцирования и дифференциального оператора Ли на этих метриках. Дана классификация переносов и перемещений метрик. Рассмотрены разложения ковариантной производной от метрики на основные структуры, имеющие отношение к связностям. Введен расширенный ковариантный дифференциальный оператор. Исследованы изменения элементарного объема под действием ковариантного оператора дифференцирования и дифференциального оператора Ли. Введены ковариантный оператор дифференцирования и дифференциальный оператор Ли, не изменяющие элементарный объем. Рассмотрены инвариантные операторы Ли и ковариантные дифференциальные операторы, действующие как изоморфизмы на контравариантные и ковариантные тензорные плотности. The theory of spaces with different contravariant
and covariant affine connections, whose components differ not only by sign,
and metrics [( Full text in PDF (611.969) |
 Home
Home
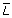 n,g)-spaces] is worked out within the
framework of the tensor analysis over differentiable manifolds and in a
volume necessary for the further considerations of the kinematics of vector
fields and the Lagrangian theory of tensor fields over
(
n,g)-spaces] is worked out within the
framework of the tensor analysis over differentiable manifolds and in a
volume necessary for the further considerations of the kinematics of vector
fields and the Lagrangian theory of tensor fields over
(