|
П. Винтернитц Монреальский университет, Канада А. А. Изместьев, Г. С. Погосян, А. Н. Сисакян Объединенный институт ядерных исследований, Дубна Лаборатория теоретической физики им. Н. Н. Боголюбова Нами введена концепция "аналитических контракций групп Ли" для связи между разделением переменных в пространствах постоянной кривизны и в евклидовом и псевдоевклидовом пространствах. Данный метод является специальной реализацией контракций типа Иноню-Вигнера, в которой радиус кривизны рассматриваемого пространства представляется в качестве параметра контракции. Для проведения контракций в явном виде параметр контракции встраивается в базис самой алгебры Ли, в оператор Лапласа-Бельтрами, в полную систему коммутирующих операторов, систему координат и решения. Это позволяет получить асимптотические соотношения между специальными функциями, связанными с группами O(n) и O(n,1), с одной стороны, и евклидовыми и псевдоевклидовыми группами - с другой. Построен также графический метод, иллюстрирующий аналитические контракции. We introduce the concept of "analytic Lie group contractions" to relate
the separation of variables in spaces of constant nonzero curvature to
separation in Euclidean or pseudo-Euclidean spaces.
These are specific realizations of In |
 Home
Home
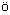 n
n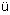 -Wigner
contractions in which
the contraction parameter is the radius of curvature of the considered space.
The parameter is introduced explicitly into the basis of the Lie algebra,
the Laplace-Beltrami operator, the complete set of commuting operators,
the coordinates themselves and the solutions. This enables
us to obtain asymptotic formulas connecting special functions related to
the groups O(n) and O(n,1) to those related to Euclidean and
pseudo-Euclidean groups. A graphical method of interpreting analytical
contractions is introduced.
-Wigner
contractions in which
the contraction parameter is the radius of curvature of the considered space.
The parameter is introduced explicitly into the basis of the Lie algebra,
the Laplace-Beltrami operator, the complete set of commuting operators,
the coordinates themselves and the solutions. This enables
us to obtain asymptotic formulas connecting special functions related to
the groups O(n) and O(n,1) to those related to Euclidean and
pseudo-Euclidean groups. A graphical method of interpreting analytical
contractions is introduced.